A Probabilistic Analysis of CASCADE (QCRYPT 2014)

Abstract

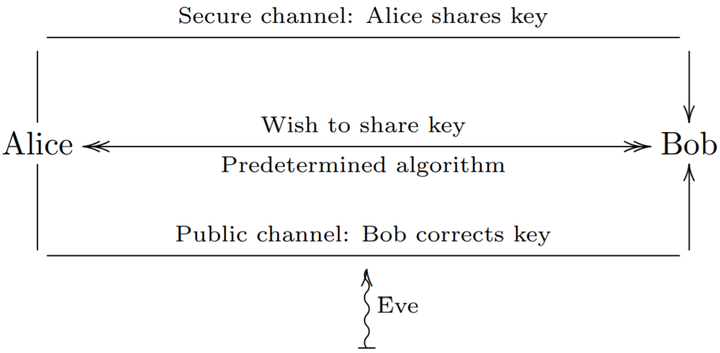
In this paper, we introduce and reconcile some of the work done on two error-correcting protocols, BINARY and CASCADE, rigorously, for a mathematically inclined audience. We also introduce our own variant of this protocol, which may be more efficient or computation-friendly, and thus a potential direction for future work. We revisit and clarify past work done in this area; in particular, we discuss proofs by Seet et al. as well as explain and critique a well-known proof by Brassard and Savail. This is supplemented with calculations that substantiate Brassard’s assumptions, and simulations of our own, to compare the protocols’ efficiencies.